Batch 2 - Class 100 - Sandpiles
Pre-Class Problem:
- (Geoffrey - 64) Mr Houseman wishes to lay down carpet on the floor of his kitchen, which is exactly 12 feet x 12 feet. He has a piece of carpet 16 feet x 9 feet, which is just enough to cover the area. However, he doesn't want to cut it in any more pieces that absolutely required. What is the minimum number of pieces he needs to cut the carpet to fit it back on the kitchen floor?
- Answer: 2 pieces
Attendance: Tishyaa, Khushi, Nandini, Muskaan
Class Notes:
Sandpiles
Stack n coins at the origin on the number line and let them spread across it according to the following rule: Identify a stack with two or more coins on it and then “fire” that stack. That is, move two coins off the identified stack and set one coin one unit to the left and the other one unit to the right. Repeat this action until there are no stacks that can fire. Here is the start of one possible sequence of moves for a game starting with a stack of six coins.
Some questions:
- Continue play with the six-coin game. What final configuration of coins do you reach?
- Play the six-coin game a second time but make different choices as to which stack to fire when. Do you end up with the same final configuration of coins? Must you?
- Must these games terminate? Could one fall into an infinite loop of fires?
- Develop a general theory about these coin firing games. Must n coins placed at the origin stabilize to the same final configuration, irrespective of the choices made along the way? If so, can you say what the final configuration must be? Can you say anything about the number of fires made along the way?
Answer:
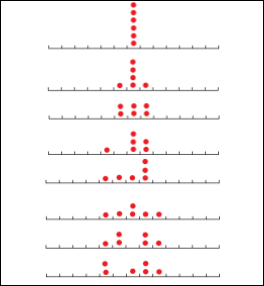
Following are the end configurations for 1-10 coin piles. The numbers below the line indicate the number of times that site fired.
.png)
- Do you notice something interesting about the number of site fires?
- These are triangular numbers!
- Can you prove that no site can fire more than its triangular number?
- Consider the first time that happens, lets say on site labeled 6. So its the 7th fire, which means 14 coins must have come to that place. But its adjacent sites have only fired 3+10 times, so it can't have 14 coins. Similarly, for the center spot, for a 16th fire, it must have 32 coins. It started with 10/11 coins, so it must get at least 21 coins more. However, its adjacent sites have only fired 20 times. Thus, no site can fire more than its triangular number times.
- How far out can the coins go. Can they go more than N/2 cells?
- No, because the penultimate cell can only fire once. Thus the N/2 cell can never get 2 coins to fire
- Hence in final state coins must be spread one each on each of the N cells.
- Which cell should be empty if we have an even number coins to start? Does it have to be the center, or can it be any other?Has to be center. Else now add a 11th coin to center, and start firing - you will cross the final N/2 cell, which is not possible
- Experiment what happens if you start with 4 coins each on adjacent cells
- You can also experiment with unequal stacks of grains, or non-adjacent stacks
- One can also play this in 2-D - by having a grid, and as soon as the number of coins on a point goes beyond the grid connectivity, it fires. Interesting patterns can form as a result of those. See http://people.reed.edu/~davidp/sand/. Following picture shows result of dropping 4 Million grains on a vertex and allowing it to settle on a grid.
.png)
Pentalpha Brain Teaser
Pentalpha game board is a 5-pointed star, and has nine chips to play with. You have to place each chip on the vertices of the board, one at a time. Each counter must touch two points before coming to rest on a third, all in straight line. The first and third points must be empty, the second point can be empty or occupied.
.png)
Can you place all the nine chips on the board?
Homework
- (Geoffrey: 113) One of the following integers, and only one, is a square. Can you find out which one? (Hint: Use Digital Roots)
3,669,517,136,205,224
1,898,732,825,398,318
4,751,006,864,295,101
5,901,643,220,186,100
7,538,062,944,751,882
2,512,339,789,576,516
- Answer: The unit digit of a square has to be 1,4,5,6,9,0 so it eliminates 2nd and 5th numbers. The digital root of a square is 1,4,7,9 - this leaves only the 6th number
References:
Mathematical Puzzles, Geoffrey Mott-Smith